Sudoku Variants

Sudoku is a puzzle that involves filling a square grid with a set of digits such that the digits are not repeated in any singular row, column or box. The most common form of sudoku is made of a 9×9 grid divided into nine 3×3 boxes. Regular sudoku may be considered hard enough, but some people have created extra rules or variants that may be used as another constraint for solvers.

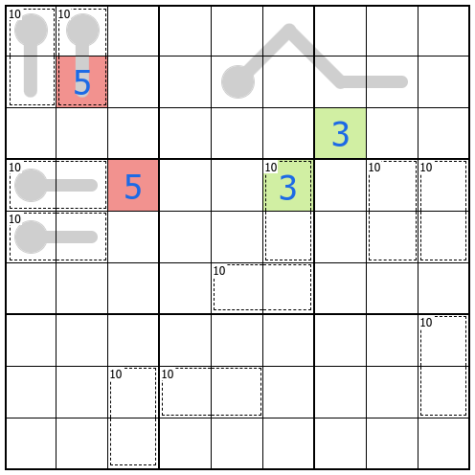
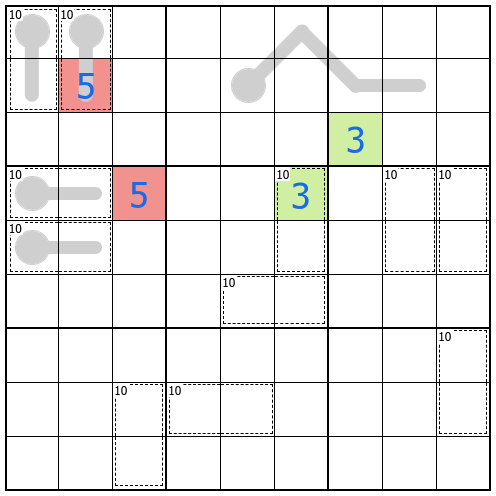
One such variant is the anti-knight’s move constraint. The rule states that cells separated by a knight’s move from chess cannot contain the same digit. Look at the first image. The 5s are separated by a knight’s move, so at least one of them is in the wrong position. On the other hand, the 3s are not sharing a row, column, box, nor knights move, so that could be a valid placement of those digits.

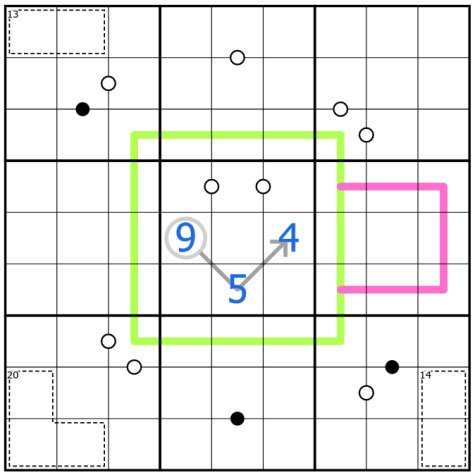
Another variant is arrows. Digits along an arrow must add up to the number in the circle at the back of the arrow. Digits along the arrow may repeat as long as such repetition is allowed by all other rules. In some specified cases, the circle may be extended to include two or more cells indicating that the sum has multiple digits. The example image shows an arrow with 4 and 5 on the arrow and a 9 in the circle because 4+5=9.

Between lines are lines with circles at both ends. The digits along the line must be between the digits in the circles. Digits along the line may repeat if allowed by all other rules. For example if 1 and 8 were in the circles, the line could contain any digit from 2, 3, 4, 5, 6, and 7, but 9 is not within the given range. I have not solved very many sudokus with a between lines variant, so I do not feel as if I have enough experience to have an opinion.

A variant with which I have played several times is a constraint on one or both of the main diagonals. The marked diagonals, often indicated with a thin blue line, cannot have repeated digits. In my experience, they can be used similarly to rows, columns, and boxes; they are just another way to rule out digits from a cell or available cells for a digit.

Another fun variant is called even/odd. Cells marked with a circle must contain an odd digit, and cells marked with a square must contain an even digit. An easy way I have found to remember which parity, whether it is even or odd, goes with which mark is that squares have an even number of sides while circles have an odd number of sides. One trick I often use with this variant is to keep track of how many digits in a row, column, or box are required to have a certain parity. In the example image, box 3 contains four cells with squares. I know that only four digits from 1-9 are even (2, 4, 6, and 8), so the rest of the cells must be odd. That means that the bottom three cells in the box are all odd. Those. combined with the two odd numbered cells in the bottom of box 2, take up all five of the odd cells in row 3, so the remaining four cells are forced to be even.

Fog of war is the name of another variant that I consider quite difficult. The grid starts covered in fog and sometimes some given digits. The fog clears when the solver places a correct digit into a cell. When such a correct digit is placed, the fog in a 3×3 area around the digit is removed. Other variants may be hidden by the fog. I have only seen it used on computerized puzzles, and I think it would be unnecessarily complicated to try to make one non-computerized. Creating one requires the computer to know the solution so that it knows when to clear the fog. The unfortunate thing about this variant is that it makes solving very easy to cheat; a solver needs only to cycle through the numbers until the fog clears. Such a method is frowned upon and considered poor sportsmanship, but that does not stop some people from cheating.

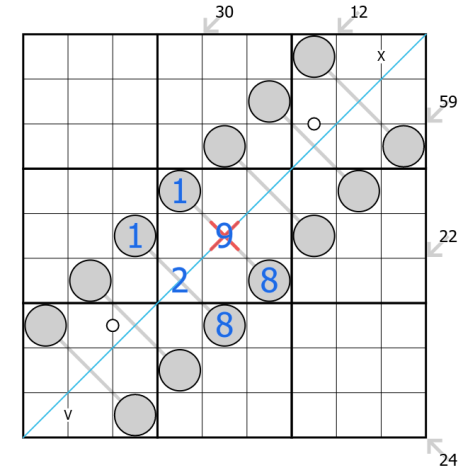
The killer sudoku variant has two varieties; killer cages and little killers. With cages, digits add to the total in the top left corner of the cage, if the sum is given. Little killers are clues placed outside the grid that give the sum of an indicated diagonal. While digits may never repeat within cages, they may repeat on little killers as shown in the example image. I do not recall ever having seen any sudokus with both little killers and cages, but they are not mutually exclusive.

Kropki dots are hollow and/or solid dots between two cells. Cells connected by a solid dot must have a ratio of 1:2. One cell’s digit must be half of the other. Cells connected by a hollow dot must be consecutive digits.

Another variant is a non-consecutive constraint. Cells that are orthogonally adjacent, that share an edge, cannot be consecutive. This variant may be used in combination with kropki dots, but there could never be any hollow dots. I have solved puzzles with this constraint several times. Like the anti-knight’s move and the diagonal variants, it can help rule out the cells where a digit can be placed.

Palindromes are another simple variant. A palindrome is a sequence that is the same forwards and backwards. Likewise, digits on a palindromic line must read the same from both directions. This can add complexity to scanning rows, columns and boxes for repeated digits; a digit might follow all rules of sudoku on one side of the palindrome while being invalid in the equivalent cell on the other side of the palindrome.

Quadruples are circles in the center of a 2×2 group of cells. The circles will contain one to four digits that must be included at least once each in the four cells touching the quadruple clue. Digits may repeat around a quadruple if allowed by all other rules. I have not personally solved very many sudokus with quadruples, so I do not have an opinion on them.

Renbans, generally shown as purple lines, must contain a string of non-repeating consecutive digits in any order. 2 and 5 cannot be on the same line unless 3 and 4 are also on the line.

Sandwiches are another variant with clues outside the grid. If 1 and 9 were slices of bread, the number in the column or row indicates the sum of the digits sandwiched between them. A 0 as a sandwich clue means that the 1 and 9 are orthogonally adjacent digits, and a 35 clue puts 1 and 9 on opposite ends of a row or column.

Skyscrapers also use clues strictly outside the grid. Imagine the digit in every cell is the height of a skyscraper placed in that cell. The clue indicates the number of skyscrapers visible in the indicated column or row from the perspective of the clue. Some skyscrapers can be hidden behind taller ones, and 9 is always the tallest and last seen skyscraper. This is another variant I have seen a few times but have never actually played. The example image is a visual diagram of the skyscrapers, which I believe would be very helpful when using such a ruleset.

Another common variant is thermometers. Thermometers must contain a set of non-repeating digits that increase from the bulb end. The adjacent numbers do not have to be consecutive, but they must not decrease or remain the same.

Whispers or German whispers are a common variant that is usually represented by green lines. Adjacent digits on the line must differ by at least five. Therefore, 5 is a digit that cannot ever appear on a German whisper; 0 and 10 are invalid in most sudokus… Another trick I have learned is that digits on the lines alternate entropies. This means that if one digit is higher than 5, the next digit must be lower than 5. I also like that some digits are restricted by the number of digits at least five away. 4 and 6 can only ever be next to a 9 and 1 respectively.

Clues outside the grid are also used with X-sums. The clues refer to a column or row. The first cell in that row or column has a value of X where the first X cells add to the value of the clue. This is again another variant that I have not seen very often, but I know that the clue can never be 2 or 4.

The last variant I would like to discuss is XVs. The letters X and V will appear like kropki dots between two orthogonally adjacent cells. I, for one, like Roman numerals, just like cells connected by a V must sum to five, and cells connected by an X must sum to ten. Just like whispers, this ruleset forces 5 to never appear on an X nor on a V. Because of this restriction on 5 placement, I use it to eliminate cells when I am solving for 5s in the grid.

There are a multitude of sudoku variants that are able to be used in puzzles. Sometimes a constructor creates a custom rule, and sometimes multiple variants can be used on the same grid. Different people enjoy different variants. They are a step up for puzzle solvers that want an increase in difficulty.